Analisis de sobrevida.3
- ruthhenquin

- 15 sept 2023
- 4 Min. de lectura

Curvas de Sobrevida o Kaplan Meier
En la mayoría de los Estudios de Cohortes es muy probable poder obtener la información precisa de la fecha en que ocurrió el evento y del día en que se censuró un sujeto.
En esta situación se pueden utilizar las curvas de Kaplan Meier para estimar la Sobrevida Acumulativa inmediatamente antes de producido cada evento individual.
Esta estimación se usa para construir una curva que tiene como característica ser escalonada, a diferencia de la curva que se podría construir con los datos de las Tablas de Sobrevida que es una curva suave sin saltos. (Fig. 1 y 2.)
Fig.1

Fig 2

En este caso la probabilidad de sobrevida se calcula en cada día en que ocurrió un evento, justo antes de que ocurra. En los días en que no hay eventos la sobrevida se considera 100 %.
A diferencia de las tablas de sobrevida, los intervalos de tiempo no son prefijados: están definidos por la ocurrencia de los eventos.
En la tabla se observan el número de sujetos vivos en cada intervalo de tiempo en que ocurrió un evento, los días en que ocurrió un evento, el número de eventos, el número de sujetos censurados.

Al inicio del estudio hay 109 sujetos, tiempo cero, sin eventos ni sujetos censurados, la sobrevida es 100 %.
El día 18 ocurre un evento (intervalo de tiempo desde el día 0 al 18). Justo antes del evento sigue habiendo 109 sujetos; si aplicamos la formula:

Si calculamos la probabilidad de muerte para el período de día 18 al 207, en que ocurre otro evento, en dicho período tenemos 108 sujetos y no contamos el evento nuevo. Calculamos la probabilidad de muerte como:
La sobrevida para este período (día 18 a 207) es de 0.99.
Para el período entre el día 207 y el 284 la probabilidad de muerte es de 0.0093 y la de sobrevida es del 0.99.
La sobrevida acumulativa al día 284 es el múltiplo de cada cálculo de sobrevida de cada intervalo de tiempo en que ocurrió un evento = 0.99 x 0.99 x 0.99 = 0.97
Si calculamos la probabilidad de muerte en el período donde no ocurrió ningún evento, por ejemplo el día 300, observaremos que ésta es igual a cero y la sobrevida igual a 1.

Las observaciones censuradas no causan reducción de la sobrevida, pero sí se tienen en cuenta para el cálculo del nº de sujetos en riesgo en el preciso momento en que ocurre una censura.
Las curvas de Kaplan Meier siempre comienzan en 1 o 100 % de sobrevida, y llegan a cero sólo si todos los sujetos han muerto o han sufrido el evento de interés.
Como toda estimación estadística, el cálculo de la probabilidad de muerte o sobrevida también tiene una variabilidad.
Es por esto que, cuando informamos que un grupo tiene una probabilidad de sufrir un evento del 97 %, debemos informar el Intervalo de Confianza del 95 %; es decir que la probabilidad puede estar en el 95 % de los casos entre dos valores, por ejemplo de 95 % a 100 %.
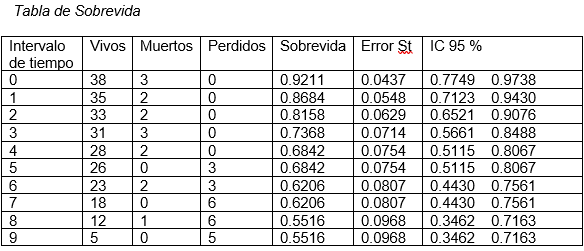
El valor de Probabilidad de Muerte también tiene un error estándar con el cual calculamos el IC 95 % y una Mediana, que en este caso se define como el momento en que la mitad de los sujetos han muerto o sufrido el evento de interés. (Tabla )
Comparación de Curvas de Kaplan Meier. Prueba Log Rank test
Supongamos que tenemos dos grupo de sujetos, un grupo con enfermedad coronario y otro sin ella.
Como vemos en la figura 24-3, los sujetos con enfermedad coronaria tiene menos sobrevida a 10 años (aproximadamente 55 % vs. 80 %)
Fig. Curvas de Kaplan Meier según enfermedad coronaria

Si queremos saber si estas diferencia son estadísticamente significativas, la prueba que debemos aplicar se llama Log Rank test.
Es muy parecido, desde el punto de vista matemático, a la prueba de Chi Cuadrado. Compara las muertes esperadas (muertes ocurridas sólo por azar) vs. las observadas en cada grupo y determina si existe diferencias significativas a través del valor de p.

De acuerdo con el valor de p obtenido podemos decidir si las curvas son diferentes o no. Lo que se desea comprobar es si la diferencia de sobrevida se debió al azar o a la presencia de enfermedad coronaria.
Si bien con el Long Rank test podemos definir si las curvas son diferentes o no, lo que no podemos es cuantificar la diferencia.
Hazard Ratio
Para determinar el riesgo de muerte que tienen los enfermos coronarios vs. los no coronarios recurrimos a la estimación de un parámetro muy parecido al Riesgo Relativo en su interpretación llamado Hazard Ratio. (HR)
Esta medida de estimación de riesgo se obtiene mediante un cálculo complejo en el cual se utiliza la Regresión de Cox.
Para el ejemplo anterior, el riesgo de muerte medido por el HR de los pacientes con enfermedad coronaria es de 2.07 con IC 95 % de 1.17 a 3.66.
Concluimos entonces que los pacientes con enfermedad coronaria tienen entre un 17 % y un 360 % más de probabilidad de morir comparado con los sujetos sin enfermedad coronaria.


Comentarios