Errores Alfa y Beta
- ruthhenquin

- 5 may 2023
- 5 Min. de lectura

Las pruebas de Significación Estadística proveen, a través del cálculo del valor p, la aceptación o rechazo de la Hipótesis Nula. En general la Hipótesis Nula establece que no hay diferencia entre los valores comparados.
En la práctica, lo que se quiere demostrar es si hay o no diferencia estadística entre los grupos a comparar.
Idealmente, la prueba utilizada debe rechazar la Hipótesis Nula de no diferencia cuando no la hay y rechazarla cuando hay diferencia.
Sin embargo, ninguna prueba es perfecta. Lo que puede suceder se describe en la “Tabla de la Verdad”. En la figura las caras felices muestran el comportamiento deseado de una prueba estadística cuando la Hipótesis Nula es aceptada y realmente no hay diferencia estadística (verdadero negativo) y cuando la Hipótesis Nula es rechazada y existe diferencia estadística (verdadero positivo).
Las caras tristes muestran la decepción que sentimos cuando una prueba estadística acepta la Hipótesis Nula de no diferencia cuando realmente la hay (falso negativo) y cuando la prueba nos dice que hay diferencias cuando realmente no la hay (falso positivo)
Tabla de la verdad

Una presentación más científica muestra las posibles clasificaciones de un resultado estadístico (aceptación verdadera, rechazo verdadero, falsa aceptación o rechazo de la Hipótesis Nula)

Cuando concluimos que no hay una diferencia estadística o que si la hay, esta conclusión puede ser errónea debido a la existencia de dos tipos de errores llamados Error Tipo I o Alfa y Error Tipo II o beta.
En terminología estadística se denomina error alfa o tipo I al falso rechazo de la Hipótesis Nula. En los Diseños Experimentales es frecuente utilizar valores de alfa = 0.05, lo que significa que asumimos la posibilidad de cometer en un 5 % un falso rechazo.
En el caso de usar un Test de Comparación de Medias cometemos un error tipo I cuando, siendo la Hipótesis Nula cierta (no hay diferencias entre medias), concluimos que hay que rechazarla y aceptar la Hipótesis Alternativa (hay diferencias en las medias).
El error beta o tipo II es la falsa aceptación de no diferencia cuando realmente la hay. El test acepta la Hipótesis Nula cuando esta es falsa.
El error tipo II es crítico debido a que el interés de un investigador es tener una alta tasa de resultados confiables. Deseamos una alta probabilidad de tener verdaderos rechazos.
Esta probabilidad se la denomina Poder Estadístico y es la inversa del error beta:
Poder = 1 – β
Generalmente el Poder Estadístico de un estudio varía entre el 80 y el 90 %, lo que significa que la probabilidad de cometer un error beta varía entre el 20 y el 10 %.
Es frecuente que estos conceptos sean difíciles de incorporar rápidamente, lo relevante es entender las consecuencias de cometer estos errores.
Recordemos que el área de aceptación se encuentra en general por consenso entre ± 2 ES, dejando como área de rechazo un 2,5 % a cada lado en la Curva de Gauss.
Esta área de rechazo también es la probabilidad de estar errados al decidir si aceptamos o rechazamos una Hipótesis Nula.
Si el valor de p acordado para rechazar una Hipótesis Nula es de 0.05, debemos asumir que podemos estar cometiendo un error en un 5 % de los casos. Si el valor de p es de 0.01 entonces asumimos que podemos equivocarnos en el 1 % de los casos.
Si la distribución de dos medias están completamente separadas no hay posibilidad de cometer ningún error. El error tipo I y II, ambos son igual a cero.
Al no haber superposición el valor de p será < 0.05; cuanto más lejos estén las dos distribuciones, menor será el valor de p, tendiendo a cero. Al mismo tiempo la posibilidad de cometer un error beta es cero, ya que, al no haber superposición, no hay posibilidad de aceptar erróneamente una Hipótesis Nula de no diferencia. Si beta es = cero, el poder estadístico es igual a 100 %, lo que significa que sabemos que tenemos 100 % de posibilidades de detectar una diferencia si está realmente existe.

En el caso que las curvas se superpongan la habilidad del test estadístico, dependerá de cuanto se superpongan las curvas.

En este ejemplo el error alfa es de 0.05 y la probabilidad de error tipo II es de 0.15 o del 15 %, que es igual al área de superposición de ambas curvas. Por lo tanto, el poder estadístico ahora es de 85 % (1 – 0.15)
Esto indica que hay sólo 85 % de probabilidad de detectar una verdadera diferencia, o a la inversa un 15 % de que, habiendo diferencia, ésta no pueda detectarse.
Para entender el concepto de Poder Estadístico hay que mirar cuánto del área de una muestra está más allá de la línea vertical que corresponde al área de rechazo del 0.05 de la otra media.
En la figura 3 toda la curva está a la derecha de la línea vertical correspondiente al área de rechazo. Por lo tanto, aquí el Poder es máximo.
En la figura 4 sólo parte de la curva está a la derecha de la línea vertical, hay un 15 % que se superpone, por lo que el Poder está disminuido.
El Poder muestra la capacidad de un experimento de detectar una diferencia de determinada magnitud. Cuanto mayor es la diferencia entre las medias, mayor poder para detectar la diferencia. Cuanta mayor superposición menor Poder estadístico. Hay que recordar que la distribución de las medias depende del tamaño de la muestra, a muestras grandes, distribuciones con base más estrecha y más probabilidad que estén separadas. Por lo tanto el tamaño de la muestra afecta directamente el error beta.
En conclusión, grandes diferencias serán fáciles de detectar y pequeñas diferencias más difícil.
Veamos dos ejemplos
En la siguiente figura las muestras tienen un tamaño relativamente grande, debido a la forma de la distribución de las medias. Con un nivel de significación estadística de 0.05, la superposición de las curvas o error beta es de 30, con un poder de 70 %

Si ahora el tamaño de las muestras disminuye, las curvas tendrán una base más ancha y aunque no se modifique el nivel de significancia, el área de superposición aumentará a un error beta de 60, con la consecuente reducción del poder a 40 %.
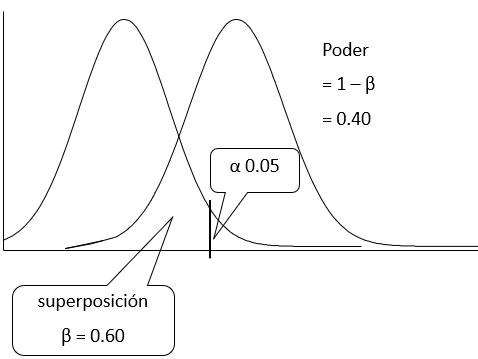
Como vemos el tamaño de la muestra tiene una influencia muy importante en el error beta y por lo tanto del poder para detectar una cierta diferencia.
Generalmente el nivel de Significación estadística o punto de corte para el rechazo de la hipótesis nula se establece en 5 %. Existe la posibilidad de disminuirlo a 0.01 o 1 %, con lo cual sólo habrá un 1 % de posibilidad de rechazar una Hipótesis Nula verdadera (1 % de aceptar diferencia cuando no la hay).
Este cambio de alfa, afecta el error beta en la dirección opuesta.
En la siguiente figura se fijo el nivel de significación en 0.05, beta es 0.30 y poder Estadístico es de 70 %.

Si el nivel de significación, con las mismas muestras se cambia a 0.01, ahora el área de superposición será de 0.50 y el poder cae a 50 %.
Por lo tanto la probabilidad de detectar una diferencia verdadera ahora es de sólo el 50 %.
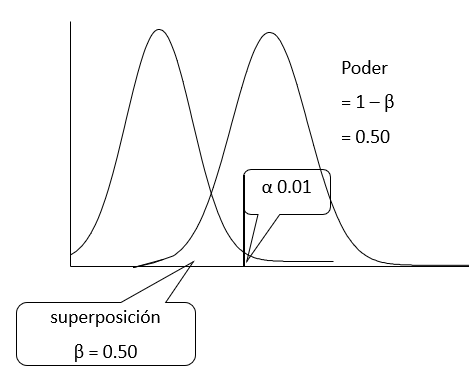
En conclusión, la elección del nivel alfa implica cambios en los valores de beta y el Poder que pueden afectar la posibilidad de llegar a una conclusión errónea. De ahí la importancia de entender este tipo de errores y sus consecuencias.
Otra forma de evitar cometer estos errores es calcular correctamente el tamaño de la muestra.


Comentarios